Vorlesungsnotizen zum 17.04.2018

Tooling

Zu Beginn des Seminars sollen euch die notwendigen Werkzeuge zur Lösung der bevorstehenden Aufgaben angereicht werden.

Eine Brute Force Lösung

#include <cstdint>
#include <iostream>
#include <gmp.h>
#include <gmpxx.h>

int main(){
 mpz_class input;
 cin << input;
 
 mpz_class line = 0;
 mpz_class linesize = 1;
 mpz_class i = 0;
 while(i < input){
  i += linesize;
  line++;
  linesize += 2;
 }
 
 mpz_class line_middle = line*line - line + 1;
 mpz_class column = input - line_middle;
 column = abs(column);
 line--;
 mpz_class result = line+column;
 cout << result << endl;
 return 0;
}

Woran erkennt man, dass diese Lösung nicht weit hilft? Messen:

• Debug by echo
• Intern Zeit messen
• Extern Zeit messen
• Manuelle Komplexitätsanalyse
• Praktische Komplexitätsanalyse

Ein Gefühl für Zeit (Debug by echo)

Fügen wir mal folgende Ausgabe in die Schleife ein:

 while(i < input){
  i += linesize;
  line++;
  linesize += 2;
  cout << i << endl;
 }

Beobachten Sie, wie schnell der untersuchte Raum anwächst.

Ab einigen Dezimalstellen wird es deutlich langsamer. Die erste Drosselung erlebt man vielleicht ab der aktuell üblichen Maschinenwortgrenze (32/64 Bit). Aber bald sollte auffallen, dass dieser Suchansatz ab einer bestimmten Größe “verhungert”. Bestimmte die Differenz an Dezimalstellen zwischen dem in einer Minute erreichten Zahlenraum mit der Eingabezahl.

Interne Zeitmessung

C++11 erlaubt folgende Zeitmessungshilfen:

std::chrono::steady_clock::time_point begin = std::chrono::steady_clock::now();
// [Zu messender Code hier]
std::chrono::steady_clock::time_point end = std::chrono::steady_clock::now();
auto duration_in_us = std::chrono::duration_cast<std::chrono::microseconds>(end - begin).count();

Testen Sie ihren Code mit mehreren Testeingaben unterschiedlicher Größe und vergleichen Sie den Zuwachs.

Vorteil(e):

• Messpunkte sehr genau einstellbar. Nachteile:
• Eingriff in das zu testende Objekt notwendig. Messen kann das Verhalten des Programms beeinflussen.

Externe Zeitmessung

Von außen betrachtet haben wir natürlich alle Möglichkeiten, die uns unser Betriebssystem so anbieten, Messungen vorzunehmen. Im Folgenden habe ich hier ein Beispiel, was uns gleich die Messung in einem angenehmen Format aufarbeitet:

#!/usr/bin/env python3

import subprocess
import time
import random
import sys

from subprocess import *

uut = sys.argv[1]

for i in range(1,128,1):
    proc_uut = subprocess.Popen([uut], stdin=PIPE, stdout=PIPE)
    # Eine zufällige Eingabe erzeugen
    input = str(random.randint(10**i, 10**(i+1))) + "\n"

    before = time.monotonic()
    out_uut = proc_uut.communicate(input.encode(), timeout=60)[0].decode()
    after = time.monotonic()
    time_uut = after-before

    print("{};{}".format(i, time_uut))

Dieses Testprogramm lässt das Programm in einer Schleife zufällige Eingabezahlen abarbeiten, nimmt die Zeit ab und dokumentiert sie im CSV Format. Das hilft uns wesentlich für eine spätere Visualisierung.

Vorteil(e):

• Besser automatisierbar
• Auch direkte Vergleiche mit Lösungen und anderen Programmen möglich
• Entkoppelt vom eigentlich zu testendem Programm Nachteile:
• Nicht so fein einstellbar in den Messpunkten. Diese sind hier fix: Direkt vor Lesen der Eingabe und direkt nach Empfangen der Ausgabe. Hier sind lastbedingte oder betriebssystembedingte Schwankungen möglich.

Manuelle Komplexitätsanalyse

Anbei diskutieren wir Zeile für Zeile den Brute-Force Code:

int main(){
 mpz_class input;
 cin << input; // Zuweisung: Konstante Zeit, pauschal eine Zeiteinheit
 
 mpz_class line = 0; // Zuweisung: Konstante Zeit, pauschal eine Zeiteinheit
 mpz_class linesize = 1; // Zuweisung: Konstante Zeit, pauschal eine Zeiteinheit
 mpz_class i = 0; // Zuweisung: Konstante Zeit, pauschal eine Zeiteinheit


 /*
  * Schleife läuft in Abhängigkeit zur Eingabe, aber in leicht modifizierter Abhängigkeit.
  * Die Schleife läuft so oft, wie die Wurzel des Eingabewerts -> n^(1/2)
  * Der Komplexitätszuwachs wird gemessen in Abhängigkeit vom Wachstum der Eingabegröße, *nicht* dem Eingabewert!
  * In welchem Stellensystem die Eingabegröße wächst, ist für Zwecke der O-Notation irrelevant.
  * Beispiel: Nehmen wir das Binärsystem, dann verdoppelt sich mit jedem Wachstumsschritt der Eingabewert.
  * Kontinuierliches Verdoppeln kann man wie folgt schreiben: 
  * 2*2*2*2*2*... -> 2^n -> Exponentielles Wachstum des Eingabewerts
  * Die Wurzel von 2^n ist 2^(n/2), was immer noch exponentiell wächst.
  */
 while(i < input){
  i += linesize; // Addition: Eine Zeiteinheit
  line++; // Addition: Eine Zeiteinheit
  linesize += 2; // Addition: Eine Zeiteinheit
 }
 
 mpz_class line_middle = line*line - line + 1; // Multiplikation, Subtraktion, Addition: Drei Zeiteinheiten
 mpz_class column = input - line_middle; // Subtraktion: Eine Zeiteinheit
 column = abs(column); // Absolutwert: Triviale konstante Operation - Pauschal eine Zeiteinheit
 line--; // Subtraktion: Eine Zeiteinheit
 mpz_class result = line+column; // Addition: Eine Zeiteinheit

 cout << result << endl; // Irrelevant, nicht Teil des Algorithmus
 return 0; // Irrelevant, nicht Teil des Algorithmus
}

Die einzige Schleife des Programms hat demnach eine exponentielle Laufzeit und definiert damit als schwerwiegenstes Element des Programms die gesamte Laufzeit: O(1) + O(2^(n/2)) = O(2^(n/2))

Praktische Komplexitätsanalyse

Wir können banal die Instruktionen mitzählen lassen, die innerhalb der Schleife passieren. Das kann beschränkt das Nachdenken (wie oben geschehen) ersetzen, erklärt einem aber nicht, wie es zum Wachstum zustandekommt.

Das Programm wird modifiziert, um die Anzahl Instruktionen auszugeben:

#include <cstdint>
#include <iostream>
#include <gmp.h>
#include <gmpxx.h>

int main(){
 mpz_class input;
 cin << input;
 
 mpz_class line = 0;
 mpz_class linesize = 1;
 mpz_class i = 0;
 
 mpz_class instructions = 0;
 
 
 while(i < input){
  i += linesize;
  line++;
  linesize += 2;
  
  instructions += 3;
 }
 
 mpz_class line_middle = line*line - line + 1;
 mpz_class column = input - line_middle;
 column = abs(column);
 line--;
 mpz_class result = line+column;
 cout << instructions << endl;
 return 0;
}

Ein Python-Testprogramm erzeugt in einer Schleife Eingaben, die in jedem Schritt um eine binäre Stelle größer wird:

#!/usr/bin/env python3

import subprocess
import time
import random
import sys

from subprocess import *

uut = sys.argv[1]

for i in range(1,128,1):
	proc_uut = subprocess.Popen([uut],stdin=PIPE, stdout=PIPE)

	input = str((2**(i+1))-1) + "\n"
	before = time.monotonic()
	out_uut = proc_uut.communicate(input.encode(), timeout=60)[0].decode()
	after = time.monotonic()
	time_uut = after-before

	out_uut = out_uut.strip()

	print("{};{}".format(i,out_uut))

Die Ausgabe sieht wie folgt aus:

1;6
2;9
3;12
4;18
5;24
6;36
7;48
8;69
9;96
10;138
11;192
12;273
13;384
14;546
15;768
16;1089
17;1536
18;2175
19;3072
20;4347
21;6144
22;8691
23;12288
24;17379
25;24576
26;34758
27;49152
28;69513
29;98304
30;139023
31;196608
32;278046
33;393216
34;556092
35;786432
36;1112184
37;1572864
38;2224368
39;3145728
40;4448733

Das Wachstum dieser Funktion sieht exponentiell aus. Online-Tools oder Mathematische Workbenchs können ein Fitting übernehmen und diesen Verdacht bestätigen.

Visualisierung der Ausgaben

gnuplot macht es sehr einfach, aus Rohdaten anschauliche Grafiken zu erzeugen. Speichern Sie die Ausgabe der manuellen Komplexitätsanlayse in ergebnis.csv und starten Sie gnuplot im selben Verzeichnis. Geben Sie die nachfolgenden Kommandos ein

set datafile separator ";"
set title "Komplexitaetsanalyse"
set ylabel "Anzahl Instruktionen"
set xlabel "Eingabegroesse in Zweierpotenz"
plot 'ergebnis.csv' with lines

Sie erhalten eine Ausgabe in einem separaten Fenster. Alternativ geben Sie als Ausgabe ein Dateiformat an:

set terminal pngcairo size 800,600
set output 'ergebnis.png'
plot 'ergebnis.csv' with lines

Und jetzt legen wir noch zwei Exponentialfunktionen an um zu sehen, ob unsere Vermutung stimmt. Mittels lw 2 heben wir unsere Funktion durch eine dickere Linie etwas hervor:

set output 'ergebnis.png'
plot 'ergebnis.csv' with lines lw 2, 2**(x/2) with lines, 2**(x/1.8) with lines

Und so sähe das dann aus:

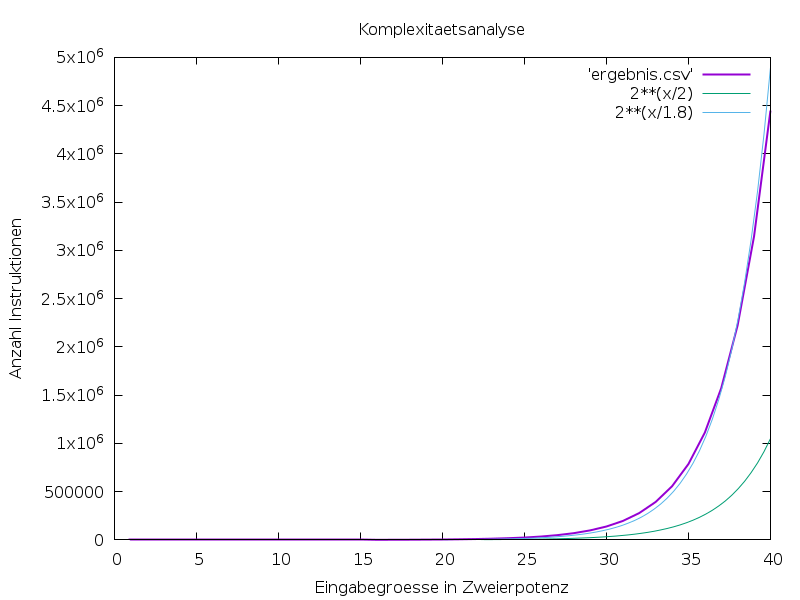
Eine “Analyse durch Draufschauen” legt also den Verdacht nahe, dass wir eine Exponentialfunktion vor uns haben. Aber Achtung: Ein Plot ist nur so gut wie die Daten, die Sie eingeben und die Annahmen, auf denen sie stehen.

Das vollständige Skript lässt sich auch als Datei abspeichern und direkt ausführen:

#!/usr/bin/env gnuplot

set datafile separator ";"
set title "Komplexitaetsanalyse"
set ylabel "Anzahl Instruktionen"
set xlabel "Eingabegroesse in Zweierpotenz"
set terminal pngcairo size 800,600
set output 'ergebnis.png'
plot 'ergebnis.csv' with lines lw 2, 2**(x/2) with lines, 2**(x/1.8) with lines