Vorlesungsnotizen zum 08.05.2018

Die Vorlesungsnotizen des vorangehenden Termins wurden überarbeitet und Ergänzungen besprochen.

Die Musterlösung zu Aufgabe 0 wurde besprochen. Sie soll als Vorlage für zukünftige Lösungen dienen.

Der Termin am 15.05.2018 wird verschoben. Am 22.05 wird eine doppelte Vorlesung stattfinden.

Problemlösungsstrategien

Wir üben die Problemlösung am Beispiel von Project Euler, Problem 83. Die Aufgabenstellung entnehmen Sie bitte von dort.

Buchempfehlung: “How to Solve it”(George Pólya, 1945)

Analysieren wir das Problem und sehen uns die Beispieleingabe an:

131 673 234 103  18
201  96 342 965 150 
630 803 746 422 111
537 699 497 121 956
805 732 524  37 331

Gesucht ist ein Weg durch ein Gitter, bei dem die kleinste Summe gebildet wird.

Gibt es dafür ein Problem aus der realen Welt?

Ja. Verallgemeinern wir das Problem. Wir wollen irgendwo hin, auf dem kürzesten Weg. Der kürzeste Weg durch einen Graphen ist ein wohldefiniertes Problem der Graphentheorie.

Können wir unser Problem auf ein Kürzester-Pfad-Problem reduzieren? Dazu müssen wir aus dieser Eingabe einen Graphen machen. Und das ist durchaus machbar:

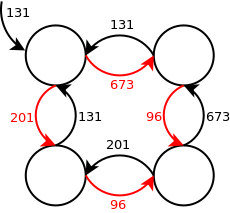
Was wir hier haben, ist ein Kantengewichteter Graph und weitere Recherche führt uns dazu, dass, da wir keine negativen Gewichte haben, der Algorithmus von Dijkstra beispielsweise bei der Lösung helfen kann.

Die tatsächliche Ausführung dieser Lösung überlasse ich euch als zusätzliche Übung.

Bei vielen Problemen, bei denen wir uns überlegen können, dass es einen Weg mit Abzweigungen geben muss, den wir beschreiten, helfen uns Algorthmen aus der Graphentheorie.

Andere Kategorien und Stichworte, die sie sich ansehen können (oder die wir kurz besprochen haben):

• Problemlösung
• Springerproblem
• Hamiltonkreisproblem
• Dynamische Programmierung
• Backtracking
• Partitionsproblem

Dies ist keine vollständige Aufzählung. Es gibt beliebig viel mehr zu entdecken.